¿Cuántas familias caben en el avión - un problema de algoritmos

Discutiremos dos soluciones al problema que se utilizó durante un cierto reclutamiento. Si puedes escribir código, te recomiendo resolverlo por tu cuenta después de leer el contenido; tomará alrededor de 10 a 30 minutos y te permitirá comparar tu solución con las presentadas a continuación:

Declaración del Problema

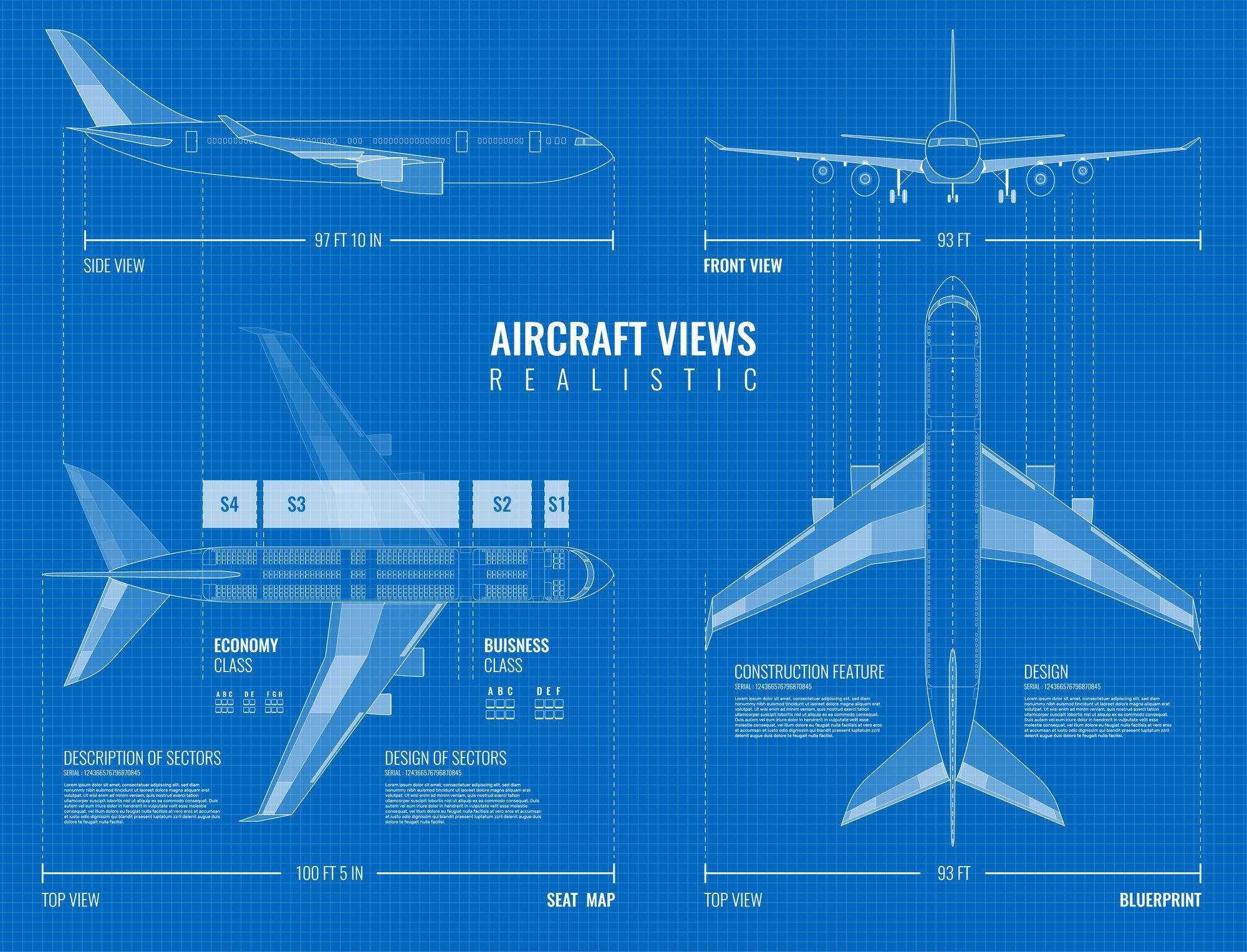
En el avión, hay asientos dispuestos en tres conjuntos que contienen 3, 4 y 3 asientos adyacentes, respectivamente. Asumimos que las filas se cuentan desde 1 y las columnas se indexan utilizando las letras del alfabeto como en una tabla de EXCEL (de la A a la K). El diagrama del avión se muestra en la imagen a continuación. Asumimos que todos los asientos tienen el mismo diseño que aquellos marcados en azul.

Asumimos que el avión tiene una longitud de N filas con asientos. También sabemos la ocupación actual de los asientos, que se registra en forma de una cadena S como coordenadas separadas por espacios del número de fila y columna, p. ej.:

S=1A 3C 2B 40G 5A

significa tomar los asientos 1A, 3C, 2B, 40G y 5A.

Nuestro objetivo es escribir una función que cuente cuántas familias de 3 personas que necesitan asientos contiguos pueden caber en el avión.

Por ejemplo, para los datos:

const S = "1A 2F 1C"
const N = 2;

el resultado correcto será 4.

Este es el mejor lugar para completar esta tarea por tu cuenta y comparar con las soluciones presentadas a continuación.

Solución de Marcin

La primera solución fue creada por mi amigo Marcin. Tiene código corto y legible. Inicializa un array bidimensional de todos los lugares, los marca con falso y finalmente itera a través de las filas contando los espacios libres según los criterios apropiados para cada uno de ellos.

function solution(N, S) {
  const seatNames = {
    'A': 0,
    'B': 1,
    'C': 2,
    'D': 3,
    'E': 4,
    'F': 5,
    'G': 6,
    'H': 7,
    'J': 8,
    'K': 9
  }
  const freeSeats = Array.from({length: N}, () => Array.from({length: 10}, () => true))
  const reservedSeats = S.split(' ');
  reservedSeats.forEach(s => {
    try {
      freeSeats[parseInt(s.substring(0, s.length - 1)) - 1][seatNames[s[s.length - 1]]] = false;
    } catch (e) {
      console.log('Some error @ reserved seat marked: ', s)
    }
  })

  let free3seats = 0
  freeSeats.forEach(rs => {
    if (rs[0] && rs[1] && rs[2]) free3seats++;
    if ((rs[3] && rs[4] && rs[5]) || (rs[4] && rs[5] && rs[6])) free3seats++;
    if (rs[7] && rs[8] && rs[9]) free3seats++;
  })

  return free3seats
}

module.exports = {solution};

Solución de Daniel

El segundo utiliza directamente un array de slots, plegándolo en una dimensión. Sin usar una estructura de datos de indexación análoga a los lugares, nos vemos obligados a calcular el índice de slot cada vez de manera secuencial, junto con declaraciones condicionales impuestas sobre las columnas. El código es más difícil de leer y requiere varias líneas de comentarios que describen la convención adoptada. Su ventaja es operar sobre una estructura de datos más pequeña, mientras que su desventaja son las declaraciones condicionales más complejas.

// DOCS
// slot 1 = empty
// slot 0 = taken
// slot "r" = taken from right
// slot "l" = taken from left

function markCorner(slots, nr, side) {
  if (slots[(nr - 1) * 3 + 1] === 1) slots[(nr - 1) * 3 + 1] = side;
  else if (slots[(nr - 1) * 3 + 1] === (side === 'l' ? 'r' : 'l')) slots[(nr - 1) * 3 + 1] = 0;
}

function solution(N, S) {
  const slots = [...new Array(3 * N)].map(() => 1);
  const places = S.split(' ');
  while (places.length) {
    const place = places.shift();
    const nr = place.slice(0, -1);
    const letter = place.charAt(place.length - 1);

    if (['A', 'B', 'C'].includes(letter)) {
      slots[(nr - 1) * 3] = 0;
    }

    if (['H', 'J', 'K'].includes(letter)) {
      slots[(nr - 1) * 3 + 2] = 0;
    }

    if (['E', 'F'].includes(letter)) {
      slots[(nr - 1) * 3 + 1] = 0;
    }

    if (['D'].includes(letter)) {
      markCorner(slots, nr, 'l');
    }

    if (['G'].includes(letter)) {
      markCorner(slots, nr, 'r');
    }
  }

  return slots.reduce((p, n) => p + Boolean(n), 0);
}

module.exports = {solution};

Comparación de Rendimiento de Soluciones

Para comparar la velocidad de ejecución de estos códigos, agregaremos un generador de coordenadas con ubicaciones:

const fs = require('fs');

function letter() {
  return ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'J', 'K'][Math.floor(Math.random() * 10)];
}

function row(N) {
  return Math.floor(Math.random() * N + 1);
}

function tempPath(N, M) {
  return `/tmp/.cache.generate-places-${N},${M}.log`;
}

// '1A 3C 2B 40G 5A'
function generatePlaces(N, M) {
  if (fs.existsSync(tempPath(N, M))) {
    return fs.readFileSync(tempPath(N, M)).toString();
  }

  let res = [];
  while (res.length < M) {
    const n = `${row(N)}${letter()}`;
    if (!res.includes(n)) {
      res.push(n);
    }
  }
  const out = res.join(' ');

  fs.writeFileSync(tempPath(N, M), out);

  return out;
}

module.exports = generatePlaces;

Las líneas de fs nos permiten guardar la lista generada de ubicaciones en caché y no regenerarla al volver a probar.

También creamos un script para probar el rendimiento de ambos algoritmos:

const d = require('./d');
const m = require('./m');
const generatePlaces = require('./generatePlaces');

if (process.argv.length !== 4) {
  throw new Error('Type `node test.js N M`');
}

const N = parseInt(process.argv[2]) || 50;
const M = parseInt(process.argv[3]) || 10;

const params = [N, generatePlaces(N, M)];

console.time('m');
const endM = m.solution(...params);
console.timeEnd('m');

console.time('d');
const endD = d.solution(...params);
console.timeEnd('d');

console.log(endM, endD);

Hipotéticamente, asumamos que tenemos un avión muy largo (quinientas mil filas). Revisaremos secuencialmente los casos de un vuelo casi vacío con 1000 asientos ocupados. El número que sigue a m es el tiempo para la solución de Marcin, y el que sigue a d es el tiempo para la de Daniel.

time node test.js 500000 1000
m: 1.339s
d: 151.637ms

Vemos que la solución que cuenta solo espacios detecta 8.8 veces más rápido. Para 20k lugares ya ocupados:

time node test.js 500000 20000
m: 1.462s
d: 276.517ms

esta ventaja cae a 5.3 veces. Si hay 40k lugares ocupados, los resultados diferirán de la siguiente manera:

time node test.js 500000 40000
m: 1.386s
d: 606.803ms

La solución de Daniel seguirá siendo más rápida, pero solo 2.2 veces. Para 80k asientos ocupados, la situación se invierte y la solución de Marcin se vuelve 1.62 veces más rápida.

time node test.js 500000 80000
m: 1.385s
d: 2.257s

En 100k lugares, el script de Marcin logra resultados que ya son 4.7 veces mejores.

time node test.js 500000 100000
m: 1.413s
d: 6.656s

Trampa

const d = require('./d');
// const m = require('./m');
const generatePlaces = require('./generatePlaces');

if (process.argv.length !== 4) {
  throw new Error('Type `node test.js N M`');
}

const N = parseInt(process.argv[2]) || 50;
const M = parseInt(process.argv[3]) || 10;

const params = [N, generatePlaces(N, M)];

// console.time('m');
// const endM = m.solution(...params);
// console.timeEnd('m');

console.time('d');
const endD = d.solution(...params);
console.timeEnd('d');

// console.log(endM, endD);

el resultado del tiempo de medición aumentará significativamente:

time node test.js 500000 100000
d: 26.454s
node test.js 500000 100000  26.42s user 0.08s system 99% cpu 26.524 total

Y de la misma manera aislada, probar el código de Marcin nos dará nuevamente el mismo resultado cercano a un segundo y medio.

time node test.js 500000 100000
m: 1.437s
node test.js 500000 100000  1.66s user 0.09s system 115% cpu 1.515 total

Para la creación de perfiles, podemos usar la bandera --porf, que creará un archivo de registro de aproximadamente 4MB.

Revisarlo no es fácil si no sabes qué buscar. Este archivo se ve algo así:

Afortunadamente, Webstorm tiene herramientas de perfilado interesantes que hacen lo mismo que esta bandera de abajo, pero aplican una superposición gráfica y gráficos que te permiten navegar por los registros y llegar rápidamente a la fuente del problema. Para configurar el perfilado, verificamos Asistencia de codificación para Node.js en la configuración.

A continuación, creamos un perfil que ejecutará nuestro script con los parámetros apropiados.

y en la pestaña V8 Profiling, seleccionamos la opción de perfilado.

Después de seleccionar el triángulo verde, comienza el perfilado.

veremos los registros ordenados por porcentaje de participación sobre el tiempo de ejecución.

Esta vista te permite extraer las funciones más que consumen tiempo en relación con el tiempo total de ejecución. Puedes leer más sobre la creación de perfiles en la documentación de WebStorm.

V8 CPU y perfilado de memoria | WebStorm

Un reexamen del código y el resumen del registro con la información de que la cantidad de espacios ocupados reduce significativamente el rendimiento del script indica que el problema debe buscarse en la función shift.

const place = places.shift();

Un hilo en stack overflow fue dedicado a esto

¿Por qué pop es más rápido que shift?

Cambiando esta línea

const place = places.shift();

en

const place = places.pop();

en el algoritmo de Daniel se restaura su ritmo correcto de operación sin importar si se ejecuta o no el código de Marcin

time node test.js 500000 100000
m: 1.449s
d: 233.327ms
1421226 1421226
node test.js 500000 100000  1.89s user 0.13s system 114% cpu 1.768 total

y

time node test.js 500000 100000
d: 238.217ms
node test.js 500000 100000  0.27s user 0.04s system 101% cpu 0.311 total

Después de una ligera modificación del código escrito por bhirt en Slack Overflow:

let sum;
const tests = new Array(8).fill(null).map((e, i) => (i + 6) * 10000);

console.log(JSON.stringify(process.versions));

tests.forEach(function (count) {
  console.log('Testing arrays of size ' + count);
  let s1 = Date.now();
  let sArray = new Array(count);
  let pArray = new Array(count);
  for (let i = 0; i < count; i++) {
    const num = Math.floor(Math.random() * 6) + 1;
    sArray[i] = num;
    pArray[i] = num;
  }
  console.log(' -> ' + (Date.now() - s1) + 'ms: built arrays with ' + count + ' random elements');

  s1 = Date.now();
  sum = 0;
  while (pArray.length) {
    sum += pArray.pop();
  }
  console.log(
    ' -> ' + (Date.now() - s1) + 'ms: sum with pop() ' + count + ' elements, sum = ' + sum
  );

  s1 = Date.now();
  sum = 0;
  while (sArray.length) {
    sum += sArray.shift();
  }
  console.log(
    ' -> ' + (Date.now() - s1) + 'ms: sum with shift() ' + count + ' elements, sum = ' + sum
  );
});

vemos que la última versión de node no solucionó este problema

{"node":"15.8.0","v8":"8.6.395.17-node.23","uv":"1.40.0","zlib":"1.2.11","brotli":"1.0.9","ares":"1.17.1","modules":"88","nghttp2":"1.42.0","napi":"7","llhttp":"2.1.3","openssl":"1.1.1i","cldr":"38.1","icu":"68.2","tz":"2020d","unicode":"13.0"}
Testing arrays of size 60000
 -> 12ms: built arrays with 60000 random elements
 -> 5ms: sum with pop() 60000 elements, sum = 209556
 -> 1057ms: sum with shift() 60000 elements, sum = 209556
Testing arrays of size 70000
 -> 20ms: built arrays with 70000 random elements
 -> 1ms: sum with pop() 70000 elements, sum = 244919
 -> 1476ms: sum with shift() 70000 elements, sum = 244919
Testing arrays of size 80000
 -> 5ms: built arrays with 80000 random elements
 -> 0ms: sum with pop() 80000 elements, sum = 279502
 -> 1993ms: sum with shift() 80000 elements, sum = 279502
Testing arrays of size 90000
 -> 4ms: built arrays with 90000 random elements
 -> 0ms: sum with pop() 90000 elements, sum = 313487
 -> 2601ms: sum with shift() 90000 elements, sum = 313487
Testing arrays of size 100000
 -> 4ms: built arrays with 100000 random elements
 -> 1ms: sum with pop() 100000 elements, sum = 350059
 -> 3263ms: sum with shift() 100000 elements, sum = 350059
Testing arrays of size 110000
 -> 8ms: built arrays with 110000 random elements
 -> 1ms: sum with pop() 110000 elements, sum = 384719
 -> 4154ms: sum with shift() 110000 elements, sum = 384719
Testing arrays of size 120000
 -> 7ms: built arrays with 120000 random elements
 -> 0ms: sum with pop() 120000 elements, sum = 419326
 -> 5027ms: sum with shift() 120000 elements, sum = 419326
Testing arrays of size 130000
 -> 8ms: built arrays with 130000 random elements
 -> 0ms: sum with pop() 130000 elements, sum = 454068
 -> 5702ms: sum with shift() 130000 elements, sum = 454068

En el navegador, estas operaciones tardan la mitad de tiempo, pero la diferencia entre pop y shift sigue siendo enorme, y cada 50-100 elementos añadidos al arreglo añaden un milisegundo al tiempo de ejecución de shift.

Al modificar este código para probar una segunda vez, podemos obtener una versión que funcione bien en el navegador y permita generar datos para dibujar un gráfico:

var sum;
var res = [];
var tests = new Array(20).fill(null).map((e, i) => (i + 1) * 10000);

tests.forEach(function (count) {
  console.log('Testing arrays of size ' + count);
  let s1 = Date.now();
  let sArray = new Array(count);
  let pArray = new Array(count);
  for (let i = 0; i < count; i++) {
    const num = Math.floor(Math.random() * 6) + 1;
    sArray[i] = num;
    pArray[i] = num;
  }
  console.log(' -> ' + (Date.now() - s1) + 'ms: built arrays with ' + count + ' random elements');

  s1 = Date.now();
  sum = 0;
  while (pArray.length) {
    sum += pArray.pop();
  }
  console.log(
    ' -> ' + (Date.now() - s1) + 'ms: sum with pop() ' + count + ' elements, sum = ' + sum
  );

  s1 = Date.now();
  sum = 0;
  while (sArray.length) {
    sum += sArray.shift();
  }
  res.push([count, Date.now() - s1]);
  console.log(
    ' -> ' + (Date.now() - s1) + 'ms: sum with shift() ' + count + ' elements, sum = ' + sum
  );
});

Generaremos un gráfico que muestre la dependencia del tiempo en la longitud del arreglo en chart.js

let res = [[10000,3],[20000,3],[30000,4],[40000,193],[50000,304],[60000,450],[70000,625],[80000,859],[90000,1081],[100000,1419],[110000,1704],[120000,2040],[130000,2466],[140000,2936],[150000,3429],[160000,3948],[170000,4509],[180000,5158],[190000,5852],[200000,6450]];

const labels = res.map(r => r[0]);
const data = {
  labels: labels,
  datasets: [{
    label: 'Time [ms] of sum of rarray computed with shift method vs array length',
    backgroundColor: 'rgb(255, 99, 132)',
    borderColor: 'rgb(255, 99, 132)',
    data: res.map(r => r[1]),
  }]
};

Reevaluación de soluciones

Originalmente, Marcin escribió un código mejor que el mío. El fallo de shift arruinó todas las mejoras de rendimiento del concepto de operar en slots en lugar de lugares individuales. Sin embargo, si permitimos el reemplazo de shift por pop en mi código (el de Daniel), resulta ser, en última instancia, varias a decenas de veces más rápido que el código de Marcin.

El archivo modificado test.js es responsable de comparar los resultados.

const d = require('./d');
const m = require('./m');
const generatePlaces = require('./generatePlaces');
const res = [];

function log(res) {
  console.log('Daniel Results');
  console.table(res.map(r => r.map(r => r.d)));
  console.log('Marcin Results');
  console.table(res.map(r => r.map(r => r.m)));
  console.log('Rations Marcin Time to Daniel Time');
  console.table(res.map(r => r.map(r => r.r)));
}

const start = new Date().getTime();

for (let N = 250000; N < 1000000; N += 250000) {
  res[N] = [];
  for (let M = 10000; M < 150000; M += 10000) {
    const params = [N, generatePlaces(N, M)];

    const sm = new Date().getTime();
    m.solution(...params);
    const em = new Date().getTime();

    const sd = new Date().getTime();
    d.solution(...params);
    const ed = new Date().getTime();
    res[N][M] = {
      d: ed - sd,
      m: em - sm,
      r: Math.round((100 * (em - sm)) / (ed - sd)) / 100
    };

    const now = new Date().getTime();
    console.log(now - start);
    log(res);
  }
}

Los resultados presentan el tiempo en milisegundos. Estos son los tiempos de Daniel, Marcin, y las proporciones del tiempo de Marcin respecto al de Daniel. Las columnas muestran el número de asientos ocupados, y las filas muestran el número de filas en el avión.