Najmniejsza wspólna wielokrotność - teoria liczb
Rozwiązanie zadania "Archery" z działu "Teoria Liczb" serwisu "Hacker Earth". Zadanie polega na wyznaczeniu najmniejszej wspólnej wielokrotności ciągu liczb.

Daniel Gustaw
• 5 min read

W serwisie Hacker Earth można znaleźć wiele ciekawych zadań dla programistów.
Jedno z nich: “Archery” prezentuję w tym wpisie wraz z omówieniem rozwiązania.
Treść zadania
Problem
N łuczników strzela strzałami do celów. Istnieje nieskończona liczba celów ponumerowanych od 1. Łucznik i strzela do wszystkich celów będących wielokrotnościami k_i.
Znajdź najmniejszy cel trafiony przez wszystkich łuczników.
Wejście
W pierwszym wierszu znajduje się liczba całkowita T - całkowita liczba przypadków testowych.
Poniżej znajdują się przypadki testowe T. Każdy przypadek testowy ma następujący format:
W pierwszym wierszu znajduje się liczba naturalna - N - liczba łuczników. Drugi wiersz zawiera N liczb całkowitych oddzielonych spacjami, gdzie każda kolejna liczba oznacza wartość k_i dla łucznika.
Wyjście
Dla każdego przypadku testowego wypisz w nowej linii najmniejszy cel trafiony przez wszystkich łuczników.
Ograniczenia
1 <= T <= 5
1 <= N <= 15
1 <= k_i <= 48

Wyjaśnienie
Pierwszy łucznik strzela do celów 2, 4, 6, 8, 10, 12, 14, …
Drugi łucznik strzela do celów 3, 6, 9, 12, …
Trzeci łucznik strzela do celów 4, 8, 12, 16, 20, …
Najmniejszym celem, do którego strzelają wszyscy łucznicy, jest 12.
Rozwiązanie
Zadzierając z problemu opowieść związaną z łucznikami zostajemy z zadaniem polegającym na znalezieniu najmniejszej wspólnej wielokrotności.
Least common multiple - Wikipedia
Kluczowe wzory to:
- Fundamentalne twierdzenie arytmetyki - każdą dodatnią całkowitą liczbę przedstawimy jako unikalny iloczyn jej czynników pierwszych z odpowiednimi potęgami

- Najmniejszą wspólną wielokrotność (lcm) pary liczb wyliczymy używając tego rozkładu

Istnieją sposoby liczenia lcm bez rozkładu na czynniki, np przez związek z największym wspólnym dzielnikiem (gcd) i algorytm euklidesa, tu jednak posłużymy się rozkładem na czynniki.
Algorytm wyznaczania Najmniejszej Wspólnej Wielokrotności
- Rozkładamy liczby na iloczyny czynników pierwszych,
- Wybieramy maksymalne krotności czynników pierwszych
- Wymnażamy czynniki pierwsze potęgując je do ilości ich wystąpień
Widzimy, że pierwszym wyzwaniem jest rozłożenie liczby na czynniki.
Rozkład liczby na czynniki pierwsze
W tym zagadnieniu bardzo pomocny jest graficzny schemat algorytmu

Ten algorytm nazywa się “Trial division” i jest najmniej oszczędnym, ale najprostszym do zrozumienia algorytmem faktoryzacji. Inne wymienione są tutaj:
Integer factorization - Wikipedia
Przed implementacją ustalmy jeszcze sposób zapisu wyniku faktoryzacji. Posłużymy się obiektem, w którym klucze to czynniki, a wartości to ilości ich wystąpień. Np do zapisania liczby 12 czyli 2 * 2 * 3 stworzymy obiekt
{
2: 2,
3: 1
}
Do wyliczenia rozkładu na czynniki będzie służył kod
function divideTimes(n, i) {
let counter = 0;
while(n % i === 0) {
counter++;
n = n / i;
}
return counter;
}
function primeFactors(n) {
if(n === 1) return { 1: 1 };
const res = {};
let p = 2
while(n >= p*p) {
if(n % p === 0) {
res[p] = divideTimes(n,p);
n /= Math.pow(p, res[p]);
} else {
p++
}
}
if(n > 1) {
res[n] = 1;
}
return res;
}
Pomijanie powtarzających się czynników w mnożeniu
W drugim kroku algorytmu mamy pomijanie powtarzających się czynników. Pokażę to na przykładzie.
Liczba 54 to 2 * 3^3, a 76 to 2^2 * 19. Ich najmniejsza wspólna wielokrotność to iloczyn 2^2 ( tu wybieramy większą potęgę ) oraz 3^3 i 19, tu wybieramy rozłączne dzielniki ( w ogólności też jest to wyższa potęga ).
Funkcję, która będzie wykonywała operację wyliczania największej wspólnej wielokrotności dla pary liczb nazwiemy
function mergeKeysChoosingMaxValue(prev, next) {
for(let key of Object.keys(next)) {
if(prev.hasOwnProperty(key)) {
prev[key] = Math.max(prev[key], next[key]);
} else {
prev[key] = next[key];
}
}
return prev;
}
Ewaluacja wartości liczby z jej czynników
Na koniec chcemy użytkownikowi wyświetlać liczby a nie ich rozkłady na czynniki, więc przejdziemy z formatu rozłożonego na czystą wartość liczbową
function evaluate(object) {
return Object.keys(object).reduce((prev, key) => {
return prev * Math.pow(Number(key), object[key]);
},1)
}
Integracja rozwiązania z formatem wejścia i wyjścia programu
Zostało nam jeszcze podłączenie napisanych przez nas części składowych do wymaganego przez zadanie formatu wejścia i wyjścia. Pierwsza część kodu odczytuje dane ze standardowego strumienia i uruchamia na nich funkcję main
process.stdin.resume();
process.stdin.setEncoding("utf-8");
let stdin_input = "";
process.stdin.on("data", function (input) {
stdin_input += input;
});
process.stdin.on("end", function () {
main(stdin_input);
});
Druga część składa się z kodu przetwarzającego linie tekstu na tablice liczb w funkcji main i wykonującego zadanie w funkcji minCommonDiv.
function minCommonDiv(k) {
const factorized = k.map(primeFactors);
return evaluate(factorized.reduce(mergeKeysChoosingMaxValue))
}
function main(input) {
const lines = input.split('\n').filter(line => Boolean(line));
const T = Number.parseInt(lines.shift());
const out = [];
for(let i=0; i<T; i++) {
lines.shift();
const k = lines.shift().split(/\s+/).map(n => Number.parseInt(n));
const res = minCommonDiv(k);
out.push(res);
}
process.stdout.write(out.join("\n") + "\n");
}
Program przy założeniu, że wejście zapiszemy do input.txt a program do app.js, nasze rozwiązanie możemy sprawdzić poleceniem:
cat input.txt | node app.js
Other articles
You can find interesting also.
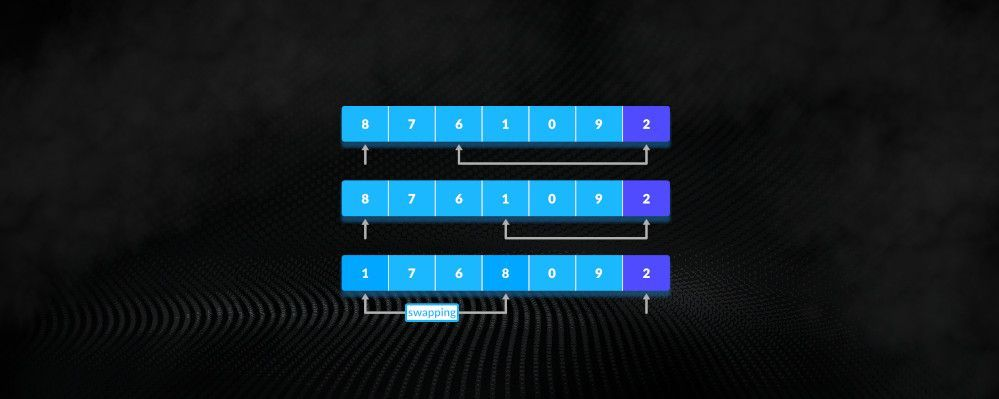
Implementacja QuickSort w Rust, Typescript i Go
Opanuj QuickSort dzięki naszemu szczegółowemu przewodnikowi oraz przykładom implementacji w trzech popularnych językach programowania, aby szybko i efektywnie sortować duże zbiory danych.

Daniel Gustaw
• 5 min read

Wyciskamy dane z PDF jak sok z cytryny
W tym wpisie pokarzemy jak pisząc naprawdę znikome ilości kodu można wygodnie wydobyć dane z plików PDF.

Daniel Gustaw
• 7 min read
Scraping Facebooka w 2021 roku
Artykuł ma na celu zapoznanie czytelnika z metodą na scaping portalu Facebooka po wprowadzeniu aktualizacji layoutu.

Daniel Gustaw
• 19 min read