Implementacja QuickSort w Rust, Typescript i Go

QuickSort to popularny algorytm sortowania, który wykorzystuje podejście dziel i zwyciężaj do sortowania tablicy elementów. Działa poprzez podział tablicy na dwie mniejsze podtablice wokół elementu pivot, który jest wybierany z tablicy. Elementy w lewej podtablicy są wszystkie mniejsze od pivota, a elementy w prawej podtablicy są wszystkie większe od pivota. Element pivot jest następnie umieszczany na swojej ostatecznej pozycji, z wszystkimi elementami po jego lewej stronie mniejszymi od niego, a wszystkimi elementami po jego prawej stronie większymi od niego. Proces ten jest powtarzany rekurencyjnie dla lewej i prawej podtablicy, aż cała tablica zostanie posortowana.

Oto podstawowe kroki algorytmu QuickSort:

1. Wybierz element pivot z tablicy. Pivot może być dowolnym elementem w tablicy, ale często wybierany jest jako pierwszy lub ostatni element.
2. Podziel tablicę na dwa podzbiory wokół elementu pivot. Wszystkie elementy mniejsze od pivotu są przenoszone do lewego podzbioru, a wszystkie elementy większe od pivotu są przenoszone do prawego podzbioru.
3. Rekursywnie sortuj lewy i prawy podzbór, używając tego samego procesu.
4. Skonkatenuj posortowany lewy podzbiór, element pivot i posortowany prawy podzbór, aby uzyskać ostateczną posortowaną tablicę.

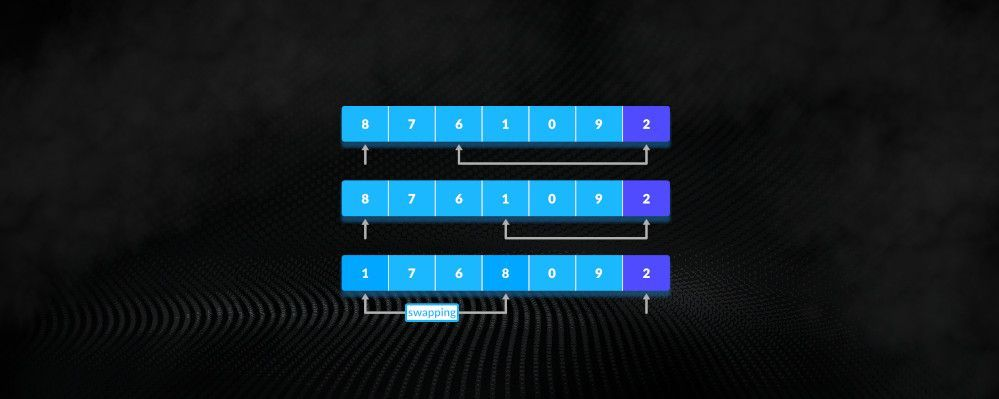
Aby podzielić tablicę, QuickSort używa podejścia z dwoma wskaźnikami, gdzie dwa wskaźniki są używane do skanowania tablicy z obu końców. Lewy wskaźnik zaczyna od pierwszego elementu tablicy i przesuwa się w prawo, podczas gdy prawy wskaźnik zaczyna od ostatniego elementu tablicy i przesuwa się w lewo. Gdy lewy wskaźnik napotka element większy lub równy pivotowi, a prawy wskaźnik napotka element mniejszy lub równy pivotowi, te dwa elementy są zamieniane miejscami. Proces trwa, aż lewy i prawy wskaźnik się spotkają, w tym momencie element pivot zostaje umieszczony na swojej finalnej pozycji.

Najgorsza złożoność czasowa QuickSort wynosi O(n^2), ale w praktyce działa znacznie lepiej niż to, ponieważ ma średnią złożoność czasową O(n log n). Wydajność QuickSort można dodatkowo poprawić, inteligentniej wybierając element pivot, na przykład wybierając medianę pierwszego, środkowego i ostatniego elementu tablicy.

Chociaż w nazwie jest Quick, nie jest to najszybszy algorytm, ale O( n log n) jest znacznie lepsze od O( n^2 ) dla popularnego prostego sortowania bąbelkowego.

Prezentuję trzy implementacje:

Quick Sort w Rust

fn quick_sort<T: Ord>(mut arr: Vec<T>) -> Vec<T> {
    if arr.len() <= 1 {
        return arr;
    }

    let pivot = arr.remove(0);
    let mut left = vec![];
    let mut right = vec![];

    for item in arr {
        if item <= pivot {
            left.push(item);
        } else {
            right.push(item);
        }
    }

    let mut sorted_left = quick_sort(left);
    let mut sorted_right = quick_sort(right);

    sorted_left.push(pivot);
    sorted_left.append(&mut sorted_right);

    sorted_left
}

fn main() {
    let arr = vec![10, 80, 30, 90, 40, 50, 70];

    println!("{:?}", arr);
    println!("{:?}", quick_sort(arr));
}

Szybkie sortowanie w TypeScript

function quickSort(arr: number[]): number[] {
    if (arr.length <= 1) {
        return arr;
    }

    const pivot = arr[0];
    const left: number[] = [];
    const right: number[] = [];

    for (let i = 1; i < arr.length; i++) {
        if (arr[i] < pivot) {
            left.push(arr[i]);
        } else {
            right.push(arr[i]);
        }
    }

    return [...quickSort(left), pivot, ...quickSort(right)];
}

// Example usage
const arr: number[] = [10, 80, 30, 90, 40, 50, 70];
const sortedArr: number[] = quickSort(arr);
console.log(sortedArr);

Szybkie sortowanie w Go

package main

import "fmt"

func quickSort(arr []int) []int {
    if len(arr) <= 1 {
        return arr
    }

    pivot := arr[0]
    left := []int{}
    right := []int{}

    for i := 1; i < len(arr); i++ {
        if arr[i] < pivot {
            left = append(left, arr[i])
        } else {
            right = append(right, arr[i])
        }
    }

    return append(append(quickSort(left), pivot), quickSort(right)...)
}

func main() {
    arr := []int{10, 80, 30, 90, 40, 50, 70}
    sortedArr := quickSort(arr)
    fmt.Println(sortedArr)
}

Wybór pivota w Quick Sort

Jest jeden problem. W początkowym opisie algorytmu wspomniałem, że wybieramy pivot. Jeśli zaczynamy z całkowicie losowymi danymi, to ten krok raczej nie ma znaczenia, ponieważ pierwszy element jest wystarczająco losowy, aby oczekiwać, że może podzielić tablicę na około podobne podtablice.

Niestety, jeśli otrzymujemy już posortowane lub prawie posortowane dane wejściowe, to użycie pierwszego elementu sprawia, że tracimy korzyści z dzielenia tablicy przy użyciu pivota, ponieważ prawie wszystkie elementy są większe od pierwszego.

Wybór elementu pivota jest krytycznym czynnikiem w wydajności QuickSort, ponieważ może mieć istotny wpływ na liczbę porównań i zamian potrzebnych do posortowania tablicy. Jeśli wybrany zostanie zły pivot, na przykład najmniejszy lub największy element w tablicy, wydajność może pogorszyć się do O(n^2), co jest znacznie wolniejsze niż przeciętna złożoność czasowa O(n log n), z której słynie QuickSort.

Aby rozwiązać ten problem, możemy łatwo zastąpić

    let pivot = arr.remove(0);

przez

    let pivot_index = arr.len() / 2;
    let pivot = arr.remove(pivot_index);

Innym, nieco bardziej zaawansowanym podejściem jest użycie mediany pierwszego, środkowego i ostatniego elementu tablicy jako pivota. Następnie:

    let pivot_index = median_of_three(&arr);
    let pivot = arr.remove(pivot_index);

i

fn median_of_three<T: Ord>(arr: &[T]) -> usize {
    let first = arr[0];
    let middle = arr[arr.len() / 2];
    let last = arr[arr.len() - 1];

    if (first < middle && middle < last) || (last < middle && middle < first) {
        arr.len() / 2
    } else if (middle < first && first < last) || (last < first && first < middle) {
        0
    } else {
        arr.len() - 1
    }
}

Z powodu problemu z wyborem pivota, QuickSort może być spowolniony przez szczególnie złośliwy wybór danych wejściowych, co czyni go podatnym na niektóre ataki bezpieczeństwa, takie jak kolizje w tabelach haszujących, jego liczne zalety sprawiają, że jest popularnym wyborem do sortowania dużych zestawów danych. Przy odpowiednim wyborze elementu pivota, QuickSort może osiągnąć średnią złożoność czasową O(n log n), co jest szybsze niż w przypadku większości innych popularnych algorytmów sortowania. Jeśli pracujesz z dużymi zestawami danych i musisz je szybko posortować, QuickSort jest doskonałym wyborem.

Wiem, co myślisz. Że ta zabawa z optymalizacją sortowania jest tylko dla naukowców, a w praktyce korzystamy z wbudowanych w naszych językach metod sortowania, ale czasami, aby zbudować coś niesamowitego, warto mieć głębszą wiedzę i intuicję, co warto optymalizować, a co nie.