Najmniejsza wspólna wielokrotność - teoria liczb
Rozwiązanie zadania "Archery" z działu "Teoria Liczb" serwisu "Hacker Earth". Zadanie polega na wyznaczeniu najmniejszej wspólnej wielokrotności ciągu liczb.

W serwisie Hacker Earth można znaleźć wiele ciekawych zadań dla programistów.
Jedno z nich: "Archery" prezentuję w tym wpisie wraz z omówieniem rozwiązania.

Treść zadania
Problem
N łuczników strzela strzałami do celów. Istnieje nieskończona liczba celów ponumerowanych od 1. Łucznik i strzela do wszystkich celów będących wielokrotnościami k_i.
Znajdź najmniejszy cel trafiony przez wszystkich łuczników.
Wejście
W pierwszym wierszu znajduje się liczba całkowita T - całkowita liczba przypadków testowych.
Poniżej znajdują się przypadki testowe T. Każdy przypadek testowy ma następujący format:
W pierwszym wierszu znajduje się liczba naturalna - N - liczba łuczników. Drugi wiersz zawiera N liczb całkowitych oddzielonych spacjami, gdzie każda kolejna liczba oznacza wartość k_i dla łucznika.
Wyjście
Dla każdego przypadku testowego wypisz w nowej linii najmniejszy cel trafiony przez wszystkich łuczników.
Ograniczenia
1 <= T <= 5
1 <= N <= 15
1 <= k_i <= 48
Wyjaśnienie
Pierwszy łucznik strzela do celów 2, 4, 6, 8, 10, 12, 14, ...
Drugi łucznik strzela do celów 3, 6, 9, 12, ...
Trzeci łucznik strzela do celów 4, 8, 12, 16, 20, ...
Najmniejszym celem, do którego strzelają wszyscy łucznicy, jest 12.
Rozwiązanie
Zadzierając z problemu opowieść związaną z łucznikami zostajemy z zadaniem polegającym na znalezieniu najmniejszej wspólnej wielokrotności.

Kluczowe wzory to:
- Fundamentalne twierdzenie arytmetyki - każdą dodatnią całkowitą liczbę przedstawimy jako unikalny iloczyn jej czynników pierwszych z odpowiednimi potęgami

- Najmniejszą wspólną wielokrotność (lcm) pary liczb wyliczymy używając tego rozkładu

Istnieją sposoby liczenia lcm bez rozkładu na czynniki, np przez związek z największym wspólnym dzielnikiem (gcd) i algorytm euklidesa, tu jednak posłużymy się rozkładem na czynniki.
Algorytm wyznaczania Najmniejszej Wspólnej Wielokrotności
- Rozkładamy liczby na iloczyny czynników pierwszych,
- Wybieramy maksymalne krotności czynników pierwszych
- Wymnażamy czynniki pierwsze potęgując je do ilości ich wystąpień
Widzimy, że pierwszym wyzwaniem jest rozłożenie liczby na czynniki.
Rozkład liczby na czynniki pierwsze
W tym zagadnieniu bardzo pomocny jest graficzny schemat algorytmu
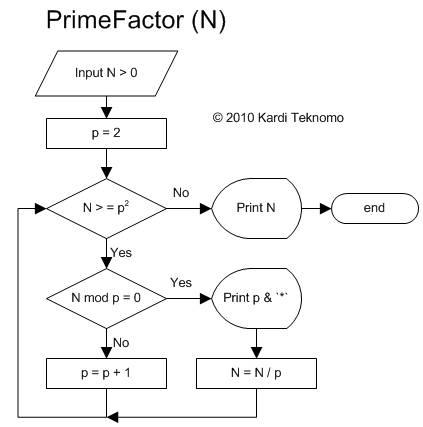

Ten algorytm nazywa się "Trial division" i jest najmniej oszczędnym, ale najprostszym do zrozumienia algorytmem faktoryzacji. Inne wymienione są tutaj:

Przed implementacją ustalmy jeszcze sposób zapisu wyniku faktoryzacji. Posłużymy się obiektem, w którym klucze to czynniki, a wartości to ilości ich wystąpień. Np do zapisania liczby 12 czyli 2 * 2 * 3 stworzymy obiekt
{
2: 2,
3: 1
}Do wyliczenia rozkładu na czynniki będzie służył kod
function divideTimes(n, i) {
let counter = 0;
while(n % i === 0) {
counter++;
n = n / i;
}
return counter;
}
function primeFactors(n) {
if(n === 1) return { 1: 1 };
const res = {};
let p = 2
while(n >= p*p) {
if(n % p === 0) {
res[p] = divideTimes(n,p);
n /= Math.pow(p, res[p]);
} else {
p++
}
}
if(n > 1) {
res[n] = 1;
}
return res;
}Pomijanie powtarzających się czynników w mnożeniu
W drugim kroku algorytmu mamy pomijanie powtarzających się czynników. Pokażę to na przykładzie.
Liczba 54 to 2 * 3^3, a 76 to 2^2 * 19. Ich najmniejsza wspólna wielokrotność to iloczyn 2^2 ( tu wybieramy większą potęgę ) oraz 3^3 i 19, tu wybieramy rozłączne dzielniki ( w ogólności też jest to wyższa potęga ).
Funkcję, która będzie wykonywała operację wyliczania największej wspólnej wielokrotności dla pary liczb nazwiemy
function mergeKeysChoosingMaxValue(prev, next) {
for(let key of Object.keys(next)) {
if(prev.hasOwnProperty(key)) {
prev[key] = Math.max(prev[key], next[key]);
} else {
prev[key] = next[key];
}
}
return prev;
}Ewaluacja wartości liczby z jej czynników
Na koniec chcemy użytkownikowi wyświetlać liczby a nie ich rozkłady na czynniki, więc przejdziemy z formatu rozłożonego na czystą wartość liczbową
function evaluate(object) {
return Object.keys(object).reduce((prev, key) => {
return prev * Math.pow(Number(key), object[key]);
},1)
}Integracja rozwiązania z formatem wejścia i wyjścia programu
Zostało nam jeszcze podłączenie napisanych przez nas części składowych do wymaganego przez zadanie formatu wejścia i wyjścia. Pierwsza część kodu odczytuje dane ze standardowego strumienia i uruchamia na nich funkcję main
process.stdin.resume();
process.stdin.setEncoding("utf-8");
let stdin_input = "";
process.stdin.on("data", function (input) {
stdin_input += input;
});
process.stdin.on("end", function () {
main(stdin_input);
});Druga część składa się z kodu przetwarzającego linie tekstu na tablice liczb w funkcji main i wykonującego zadanie w funkcji minCommonDiv.
function minCommonDiv(k) {
const factorized = k.map(primeFactors);
return evaluate(factorized.reduce(mergeKeysChoosingMaxValue))
}
function main(input) {
const lines = input.split('\n').filter(line => Boolean(line));
const T = Number.parseInt(lines.shift());
const out = [];
for(let i=0; i<T; i++) {
lines.shift();
const k = lines.shift().split(/\s+/).map(n => Number.parseInt(n));
const res = minCommonDiv(k);
out.push(res);
}
process.stdout.write(out.join("\n") + "\n");
}Program przy założeniu, że wejście zapiszemy do input.txt a program do app.js, nasze rozwiązanie możemy sprawdzić poleceniem:
cat input.txt | node app.js


