Implementación de QuickSort en Rust, Typescript y Go

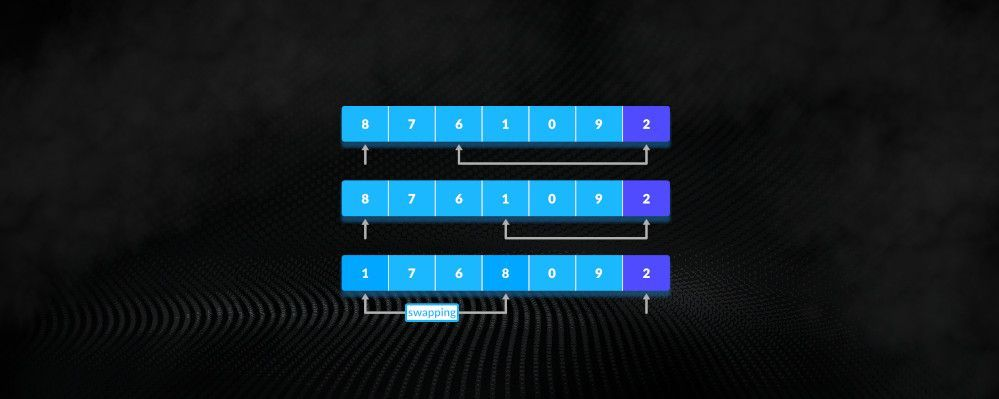
QuickSort es un algoritmo de ordenamiento popular que sigue el enfoque de divide y vencerás para ordenar un conjunto de elementos. Funciona dividiendo el arreglo en dos sub-arreglos más pequeños alrededor de un elemento pivote, que se selecciona del arreglo. Los elementos en el sub-arreglo izquierdo son todos menores que el pivote, y los elementos en el sub-arreglo derecho son todos mayores que el pivote. Luego, el elemento pivote se coloca en su posición final, con todos los elementos a su izquierda siendo menores que él, y todos los elementos a su derecha siendo mayores que él. Este proceso se repite recursivamente en los sub-arreglos izquierdo y derecho hasta que todo el arreglo esté ordenado.

Aquí están los pasos básicos del algoritmo QuickSort:

1. Elige un elemento pivote del array. El pivote puede ser cualquier elemento en el array, pero a menudo se elige el primer o el último elemento.
2. Particiona el array en dos sub-arrays alrededor del elemento pivote. Todos los elementos más pequeños que el pivote se mueven al sub-array izquierdo, y todos los elementos mayores que el pivote se mueven al sub-array derecho.
3. Ordena recursivamente el sub-array izquierdo y el sub-array derecho utilizando el mismo proceso.
4. Concatena el sub-array izquierdo ordenado, el elemento pivote y el sub-array derecho ordenado para producir el array final ordenado.

Para particionar el array, QuickSort utiliza un enfoque de dos punteros, donde se utilizan dos punteros para escanear el array desde ambos extremos. El puntero izquierdo comienza desde el primer elemento del array y se mueve hacia la derecha, mientras que el puntero derecho comienza desde el último elemento del array y se mueve hacia la izquierda. Cuando el puntero izquierdo encuentra un elemento mayor o igual que el pivote, y el puntero derecho encuentra un elemento menor o igual que el pivote, los dos elementos se intercambian. El proceso continúa hasta que el puntero izquierdo y el puntero derecho se encuentran, momento en el cual el elemento pivote se coloca en su posición final.

La complejidad temporal en el peor de los casos de QuickSort es O(n^2), pero en la práctica, se desempeña mucho mejor que esto porque tiene una complejidad temporal en el caso promedio de O(n log n). El rendimiento de QuickSort se puede mejorar aún más seleccionando el elemento pivote de manera más inteligente, por ejemplo, eligiendo la mediana del primer, del medio y del último elemento del array.

Aunque en nombre hay Quick, no es el algoritmo más rápido, pero O( n log n) es mucho mejor que O( n^2 ) para el popular y simple ordenamiento burbuja.

Presento tres implementaciones:

Ordenamiento Rápido en Rust

fn quick_sort<T: Ord>(mut arr: Vec<T>) -> Vec<T> {
    if arr.len() <= 1 {
        return arr;
    }

    let pivot = arr.remove(0);
    let mut left = vec![];
    let mut right = vec![];

    for item in arr {
        if item <= pivot {
            left.push(item);
        } else {
            right.push(item);
        }
    }

    let mut sorted_left = quick_sort(left);
    let mut sorted_right = quick_sort(right);

    sorted_left.push(pivot);
    sorted_left.append(&mut sorted_right);

    sorted_left
}

fn main() {
    let arr = vec![10, 80, 30, 90, 40, 50, 70];

    println!("{:?}", arr);
    println!("{:?}", quick_sort(arr));
}

Ordenamiento Rápido en TypeScript

function quickSort(arr: number[]): number[] {
    if (arr.length <= 1) {
        return arr;
    }

    const pivot = arr[0];
    const left: number[] = [];
    const right: number[] = [];

    for (let i = 1; i < arr.length; i++) {
        if (arr[i] < pivot) {
            left.push(arr[i]);
        } else {
            right.push(arr[i]);
        }
    }

    return [...quickSort(left), pivot, ...quickSort(right)];
}

// Example usage
const arr: number[] = [10, 80, 30, 90, 40, 50, 70];
const sortedArr: number[] = quickSort(arr);
console.log(sortedArr);

Ordenamiento Rápido en Go

package main

import "fmt"

func quickSort(arr []int) []int {
    if len(arr) <= 1 {
        return arr
    }

    pivot := arr[0]
    left := []int{}
    right := []int{}

    for i := 1; i < len(arr); i++ {
        if arr[i] < pivot {
            left = append(left, arr[i])
        } else {
            right = append(right, arr[i])
        }
    }

    return append(append(quickSort(left), pivot), quickSort(right)...)
}

func main() {
    arr := []int{10, 80, 30, 90, 40, 50, 70}
    sortedArr := quickSort(arr)
    fmt.Println(sortedArr)
}

Selección de pivote en Quick Sort

Hay un problema. En la descripción inicial del algoritmo mencioné que estamos seleccionando un pivote. Si comienzo con datos totalmente aleatorios, entonces este paso no importa mucho, porque el primer elemento es lo suficientemente aleatorio como para esperar que pueda dividir el arreglo en subarreglos aproximadamente similares.

Desafortunadamente, si estamos obteniendo una entrada ya ordenada o casi ordenada, entonces usar el primer elemento hace que perdamos la ventaja de dividir el arreglo utilizando un pivote, porque casi todos los elementos son mayores que el primero.

La elección del elemento pivote es un factor crítico en el rendimiento de QuickSort, ya que puede tener un impacto significativo en el número de comparaciones e intercambios necesarios para ordenar el arreglo. Si se elige un mal pivote, como el elemento más pequeño o el más grande en el arreglo, el rendimiento puede degradarse a O(n^2), lo que es mucho más lento que la complejidad de tiempo en el caso promedio de O(n log n) por la que QuickSort es conocido.

Para solucionar este problema, podemos reemplazar fácilmente

    let pivot = arr.remove(0);

por

    let pivot_index = arr.len() / 2;
    let pivot = arr.remove(pivot_index);

Otro enfoque un poco más sofisticado es usar la mediana del primer, medio y último elemento del array como el pivote. Entonces:

    let pivot_index = median_of_three(&arr);
    let pivot = arr.remove(pivot_index);

y

fn median_of_three<T: Ord>(arr: &[T]) -> usize {
    let first = arr[0];
    let middle = arr[arr.len() / 2];
    let last = arr[arr.len() - 1];

    if (first < middle && middle < last) || (last < middle && middle < first) {
        arr.len() / 2
    } else if (middle < first && first < last) || (last < first && first < middle) {
        0
    } else {
        arr.len() - 1
    }
}

Debido a este problema con la selección de pivote, QuickSort puede desacelerarse debido a una selección especialmente maliciosa de datos de entrada, por lo que es susceptible a algunos ataques de seguridad, como las colisiones de tablas hash. Sin embargo, sus muchas ventajas lo convierten en una opción popular para ordenar grandes conjuntos de datos. Con la elección correcta del elemento pivote, QuickSort puede alcanzar una complejidad de tiempo en caso promedio de O(n log n), que es más rápido que la mayoría de otros algoritmos de ordenamiento populares. Si estás trabajando con grandes conjuntos de datos y necesitas ordenarlos rápidamente, QuickSort es una excelente opción.

Sé lo que piensas. Que esta diversión con la optimización de ordenamiento es solo para científicos, y que en la práctica estamos utilizando algoritmos de ordenamiento integrados en nuestros lenguajes, pero a veces, para construir algo asombroso, vale la pena tener un conocimiento y una intuición más profundos sobre qué vale la pena optimizar y qué no.